[無料ダウンロード！ √] 積分 面積 マイナスになる 265356-積分 面積 マイナスになる

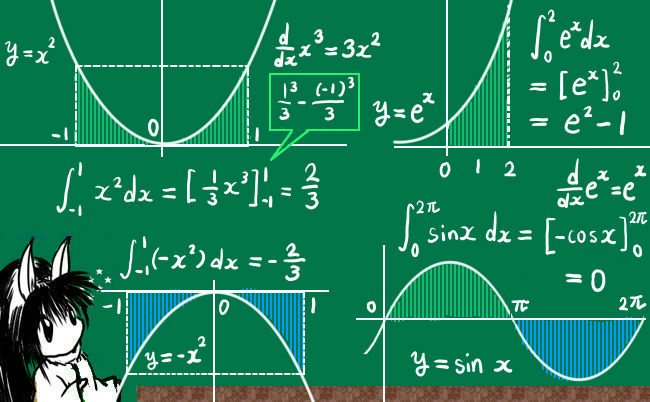
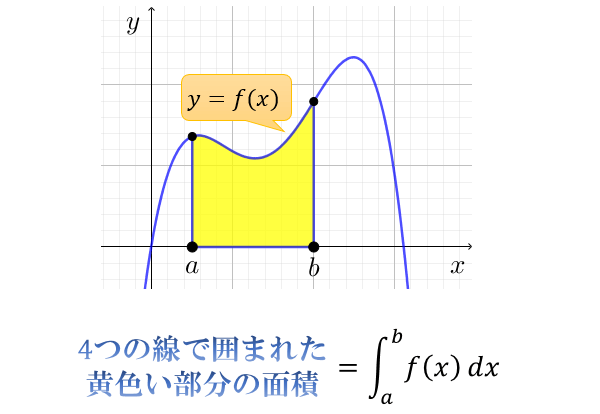
なぜ原始関数を使うのか，なぜ差なのか，そんなことをして何になるのか （教科書の項目として面積の項目は定積分の後に登場するが，）原始関数 F(x) は，関数 f(x) (>0) の下にできる図形の面積を表わし， F(b)−F(a) で a ≦ x ≦ b の区間の面積を表わせるので，このように定義すると豊かな応用P=0にすれば①になる！ （解の差の3乗）×（ 2次関数の 6 1 絶対値をとればいい。 2次の係数）に をかけて 1次関数の係数は関係ない！ （解の差の3乗）×（ 2次関数の 12 1 値をとればいい。 2次の係数）に をかけて絶対 （y軸に平行な直線接点）の3乗× 3 1 面積がマイナス？色々な解釈で面積を正確に求める 積分で変な形の面積も求められるようになるとかなり自由に面積が求められるようになりそうなものですが、注意しなければいけないことがいくつかあります。 その1つが 求める面積の場所 です。

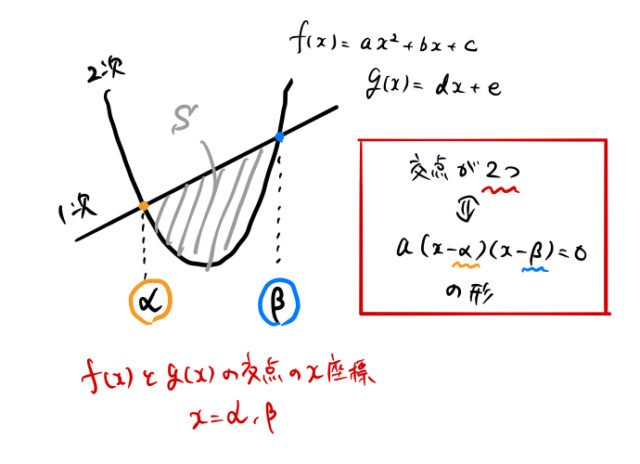
数ii積分 曲線にかこまれた図形の面積を求める 解と係数の関係が成り立つ仕組み 北海道大18 Mm参考書

積分 面積 マイナスになる

積分 面積 マイナスになる-和S(∆;γ) は, 上のような短冊の面積として与えられる 12 積分の定義 さて, 11節では, 積分区間a,b の分割∆ と各小区間の代表点γ を与えることにより, 底辺が∆xi で高さがf(γi) の長方形からなる短冊を考え, この短冊の面積として, Riemann 和S(∆;γ) を定義し 定積分がマイナスになるかどうか だけです。 ただの定積分を求めるために解く定積分の計算はマイナスになることがありますが、 面積を求めるために使う定積分では、マイナスになることはありません。 定積分$\,\displaystyle \int_{a}^{b}f(x)dx\,$の場合は、xで

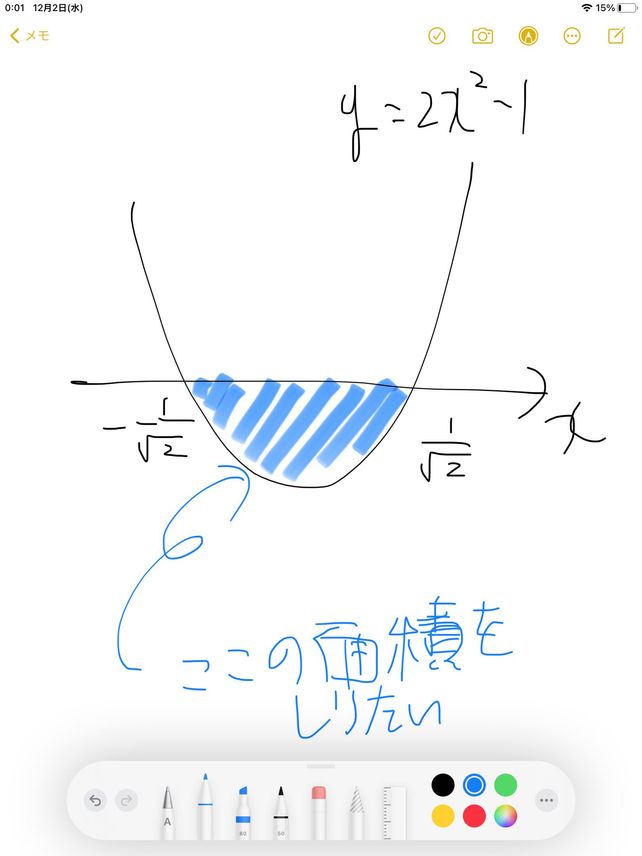
15 X S Lihat Cara Penyelesaian Di Qanda

 定積分で面積を求める① 定積分の計算の仕方を前回の記事で紹介しました。 定積分自体は計算の1種であり、正しく計算するとマイナスの数、負の数が答えになることもあります。 今回は、定積分の計算を使って求められることを1つ紹介します。 目次∫ f (x) dx （ f (x)の a から b までの定積分）で面積を求めようとしたら，マイナスがついてしまいました。このページでは，なぜ定積分で面積を求めることができるのかについて，丁寧にかつ厳密に説明します． 厳密に示しますので， 数Ⅲの極限既習者向け です．このページは練習問題等はありません．

ベクトル場を積分する場合には、 線積分と面積分の2通りの方法がある。 どちらもベクトルを積分して、結果はスカラーになる。 これらはともに物理のいろいろなところで現れる重要な積分である。 まず線積分 定積分の面積を求めるとき二乗とかの後にマイナスが付いてたら〰を引いてるとこにマイナスは大体の問題 ベストアンサー：koubenessecojp/nigate/math/a14m1402html 1 19/6/22これは、面積 の微分が関数の値 になるという式です。すなわち、積分定数の自 由度を除いて、面積 は関数の値 の積分になるということです。つまり、 f(x) の 積分関数を F (x) c として以下のようになります。 S ³ f dx F(x ) c さらに、面積 S(x) は x a において

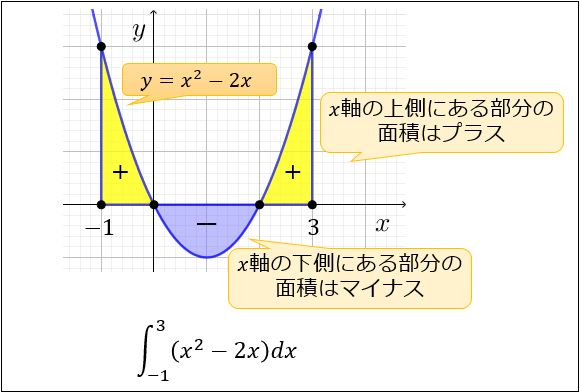
面積積分の応用：ガウス積分 面積積分を使う計算の応用の変わった例として、ガウス積分 \begin{equation} I= \int_{\infty}^\infty \coldx \E^{\xcol{x}^2} \end{equation} を取り上げよう。これは1次元積分で、面積分ではないが、面積分の手法を使うことでこの積分が計算 下図の赤い図形と比べると黄色の面積が \(\dfrac{14}{3}\) くらいになるのを実感できます。 x軸の下側の部分の面積はマイナス $\displaystyle \int_{1}^3 (x^22x) dx$ は、下図の 黄色い部分の面積 から 青い部分の面積 を 引いた値 を求めることを意味します。連絡先 kantaro@momosonetnejpツイッター http//twittercom/Kantaroお勧め動画自然対数の底e ネイピア数を東大留年美女＆早稲田

積分法 定積分と不等式の証明について 日々是鍛錬 ひびこれたんれん

数2 定積分の範囲です ぐちゃぐちゃで申し訳ないのですが教えてください Clear

また， この場合は積分区間の下端が α \alpha α なので x − α x\alpha x − α を基準にするテクニックの威力が倍増 しています（積分された関数に x = α x=\alpha x = α を代入すると0になるので面倒な計算定するだけです。）さらに、スカラー場の面積分のときと違って、曲面s に表裏を決めます。この 設定で、ベクトル場f⃗ の曲面s での面積分を、 単位時間にs を裏から表へ通過した水の量 になるように定義したいのです。Wolfram言語には，非常に強力な積分のシステムが含まれている．標準の数学関数で行える積分についてはそのほとんどすべてを行うことができる． 不定積分 を計算するためには， Integrate を使うとよい．第1引数は関数で，第2引数は変数である：

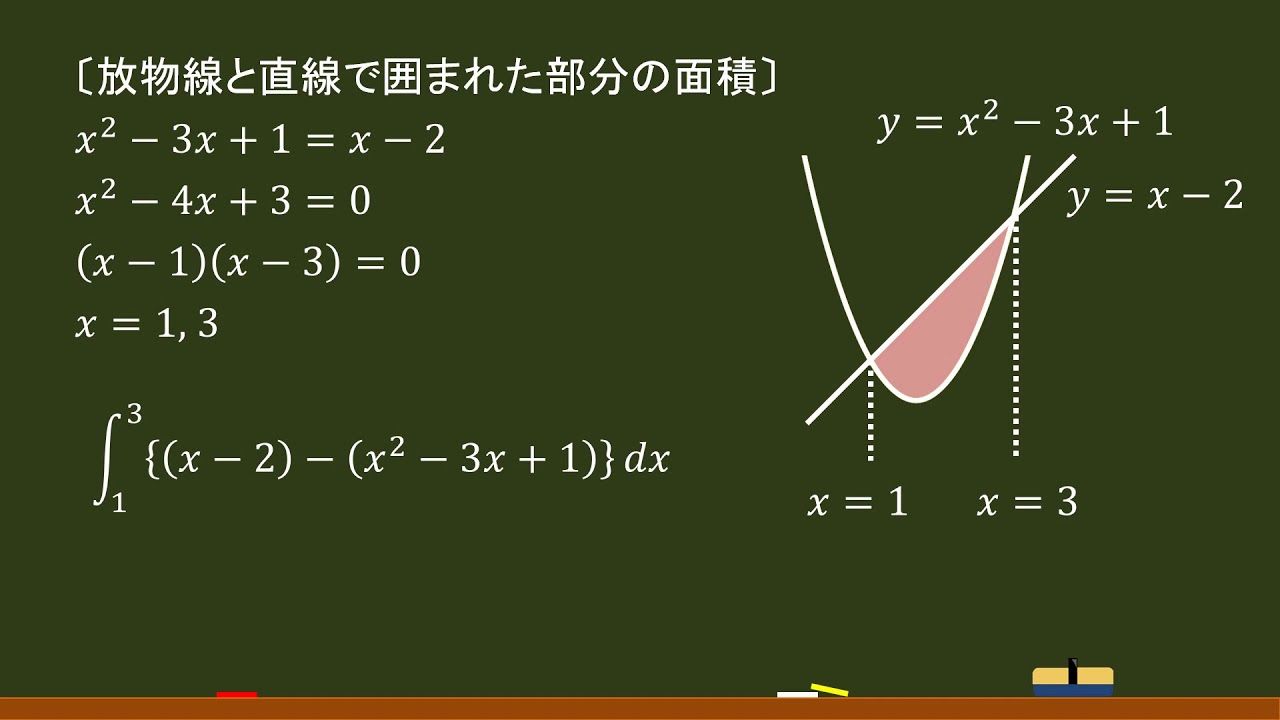
数 積分法 放物線と直線で囲まれた部分の面積 1 6公式の利用 オンライン無料塾 ターンナップ Youtube

高校数学 定積分の計算の工夫 映像授業のtry It トライイット

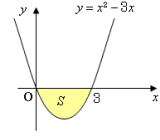
 面積分で出た値って負になることあるんですか？正になることも負になることもよくあります。面積分が実際の問題で出てくる場合、被積分関数はベクトル場であって、lim Σ F・ n ΔSのような形で登場するのが普通です。さらに、面には向きが の場合 面積をSとした場合 S=∫ 0→2 (x²2ｘ)dx= (1/3x³x²)∫ 0→2=8/34=4/3とマイナスになりますね。積分 面積 マイナス また、マイナス3分のa>1というのもどこをどのように計算をして出たのか教えてください。 積分の応用なのですが、この問題だけわかりません。 よろしければ教えてください。 積分 面積 裏技公式 早見チャート 面積 を求めよう。

矩形法 長方形近似 による数値積分 Vcssl

定積分によって面積を求める問題の解き方と公式

 マイナスには注意 してください。これはまさしく 1/6 公式が使える形です。 つまり 二次関数と x 軸が囲む面積は必ず 1/6 公式を使える形になる のです。なぜなら交点を出す式が必ず積分をする関数とほぼ同じになるからですね。 ＞x座標0からrまでの面積 x=0 では無限大になるので求まりません。 0 なぜ定積分で面積が求まるのか レベル ★ 入試対策 積分 更新日時 面積は「微分の逆の操作」を用いて求めることができる。 一見面積とは無縁な微分という操作の逆を考えることで面積が求められるというのは驚きです。

積分の考え方と基本計算 理数系無料オンライン学習 Kori

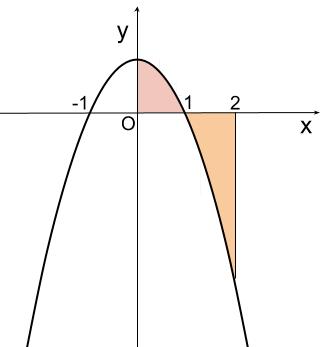
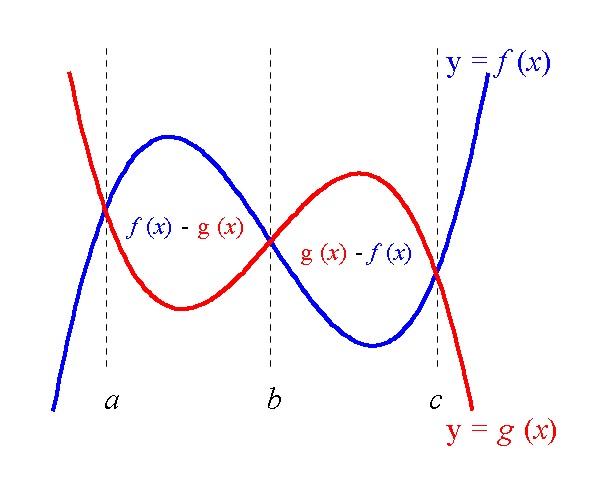
X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

41 積分とは何か 積分とは何か？ と尋ねると 微分の逆です と答える人が多い。 それは間違いではないが、実際のところは微分には微分の、積分には積分の、それぞれの意味があって、その意味が「逆」であることを示している。 ,x軸,y軸が作る図形の面積Sを求めなさい。 解き方 壁のようなx=0,x=1が作られました。 区間0,1の中でyの正負が切り替わるかどうかで積分区間を区切る必要が出てきます。 面積は被積分関数が負のときマイナス倍する必要があるからですね。 解説1．積分したい関数が「2つの関数の掛け算」である 2．片方の関数が微分すると簡単な関数になる （もう片方は積分しても余り複雑にならない関数だと嬉しい） 部分積分法（つづき） 積分 " orj微分 掛け算されている関 数をそれぞれ微分・

積分法 定積分と不等式の証明について 日々是鍛錬 ひびこれたんれん

定積分 佐々木数学塾

Sin4xはこういうグラフになる。 で、積分って言うのはだな。軸から上の部分の面積を正として数えているんだ。下の部分は当然負になって出てくる。 だから、0になるってことは、この赤と水色の面積が等しいってことだな。 ってことで正解。杉浦『解析入門I』 f(x)は閉区間I上可積とする。 a,b∈Iとするとき、以下の記法を定義する。 注意右辺の積分記号は、向きのない定積分を示す。 ※なぜ、向きの付いた定積分を定義するのか？

面積分解き方 面積公式 6分の1等 をうまく使う方法を解説 數2積分法 Pbhcl

定積分と面積 高校数学の無料オンライン学習サイトko Su

1 6公式の使い方と記述の書き方のコツ ラディカル高校数学

積分とは何なのか 面積と積分計算の意味 アタリマエ

積分 ２つの曲線の間の面積を求める公式の証明 数学ii By ふぇるまー マナペディア

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

積分とは何なのか 面積と積分計算の意味 アタリマエ

積分で面積を求める問題です 高校の授業で 面積が全部x軸より下にある場 Yahoo 知恵袋

積分法 定積分編 定積分でグラフの面積を求める ますますmathが好きになる 魔法の数学ノート

積分の問題でなぜかマイナスになる面積 19年04月05日のその他のボケ ボケて Bokete

積分の考え方と基本計算 理数系無料オンライン学習 Kori

高校数学について 積分における6分の1公式ってなぜマイナス6分の Yahoo 知恵袋

Q Tbn And9gcqoe6nsji Rx8v2ojhj51motkq Iaqslrejrf0db8emklcii6qg Usqp Cau

積分の考え方と基本計算 理数系無料オンライン学習 Kori

48s96ub7b0z5f Net Teisekibun Menseki Kihon

マイナス６分のの公式 定積分と面積 高校数学 Youtube

積分

６分の１ １２分の１ ３分の１ A Day In Our Life

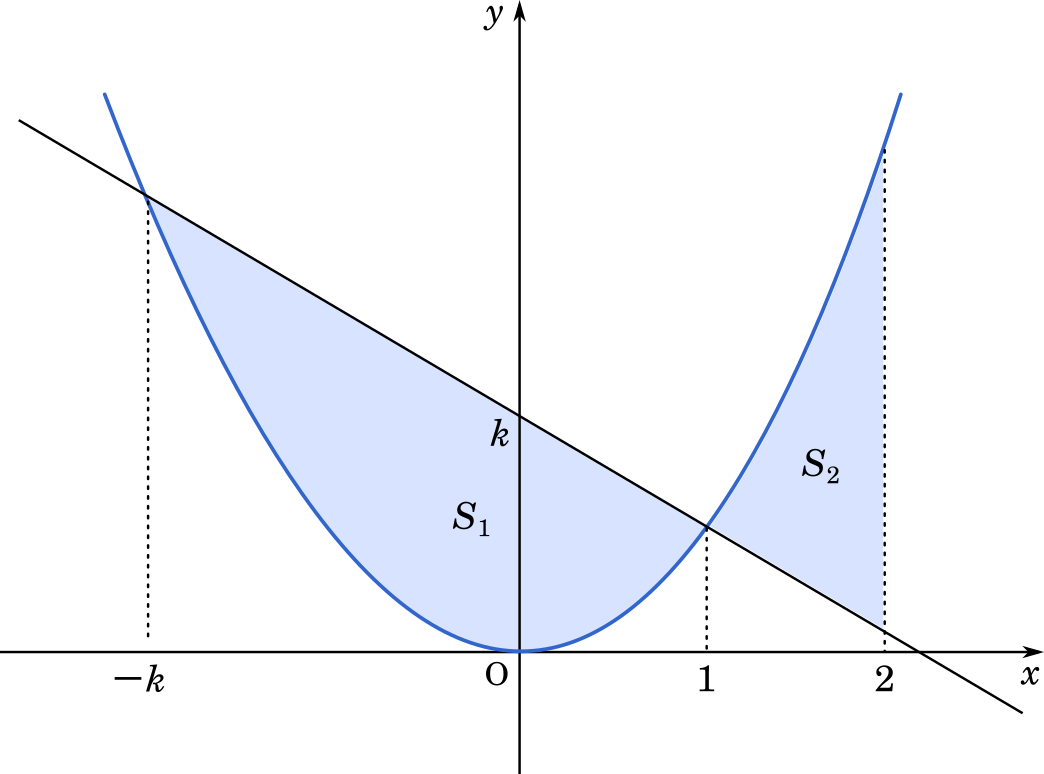
北海道大21文系第4問 数iib微分積分 6分の1公式で突破 二次関数と直線で囲まれた面積の求め方 基本レベル Mm参考書

高校数学 X A M X B Ndxの計算技巧と1 6 1 12 1 30公式 受験の月

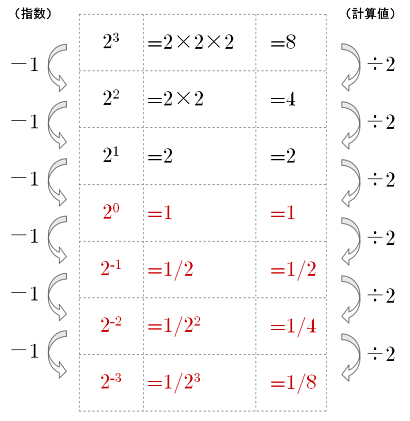
対数 ゼロの指数 マイナスの指数 大人が学び直す数学

面積がマイナスになる図形はありますか Quora

数ii積分 曲線にかこまれた図形の面積を求める 解と係数の関係が成り立つ仕組み 北海道大18 Mm参考書

数学の積分問題 解き方のコツ 公式 スタディサプリ大学受験講座

面積の計算について 数学 苦手解決q A 進研ゼミ高校講座

なぜ定積分で面積が求まるのか 高校数学の美しい物語

高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

積分の面積公式を分かりやすく解説 まず理解して覚えよう 大学生の勉強部屋

積分がマイナスになる場合 どうしても値がマイナスになってしまい Yahoo 知恵袋

15 X S Lihat Cara Penyelesaian Di Qanda

積分とは 対数とは 微分とは 分かる とはどういうことか Togetter

勉強しよう数学 微分積分はどうすれば勉強できるか ２

利用者 すじにくシチュー リーマン積分に基づく高校数学の微分積分 Wikibooks

位置 速度 加速度と積分 高校物理の備忘録

勉強しよう数学 微分積分はどうすれば勉強できるか ２

高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

3

積分してwi Fiをつなげよう 数学 統計教室の和から株式会社

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

自然科学のための数学14年度第12講

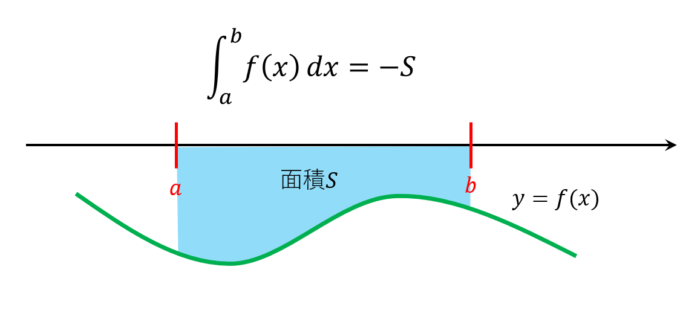
定積分のイメージ ぽこラボ勉強ブログ

微分 高階微分とマイナスの指数 大人が学び直す数学

面積の計算について 数学 苦手解決q A 進研ゼミ高校講座

６分の１ １２分の１ ３分の１ A Day In Our Life

数2 定積分の範囲です ぐちゃぐちゃで申し訳ないのですが教えてください Clear

面積を積分して求めた時に答えがマイナスになってしまったら 面積がマイナスになる訳無 Clear

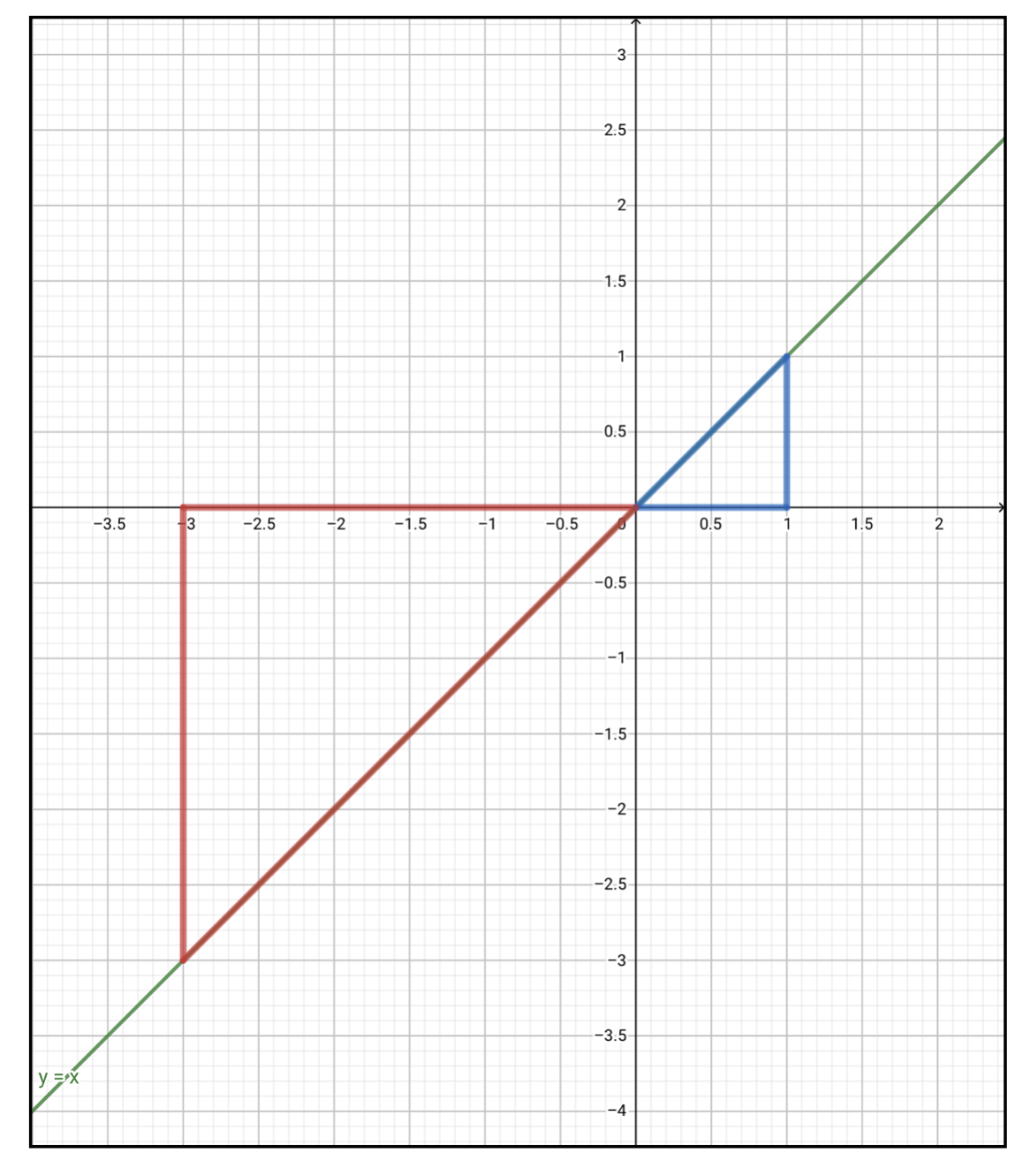
高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら

符号付きの面積ってなに ー定積分で面積がマイナスになる理由 Youtube

面積がマイナスになる図形はありますか Quora

授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する

数ii積分 定積分と面積について 初歩的な質問 定積分２曲線間の面積 数学 教えて Goo

3

基本 曲線とx軸の間の面積と積分 なかけんの数学ノート

定積分で面積を求める 一歩一歩ぐんぐんブログ

面積分解き方 面積公式 6分の1等 をうまく使う方法を解説 數2積分法 Pbhcl

3

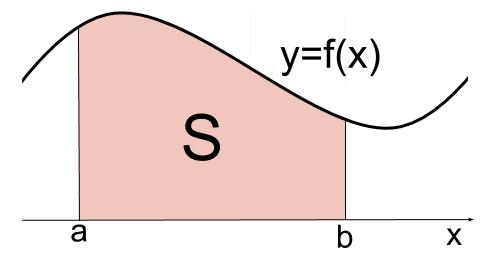
定積分と面積 高校数学の無料オンライン学習サイトko Su

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

積分面積計算機 ツールと計算機 Azyvp

48s96ub7b0z5f Net Teisekibun Menseki Kihon

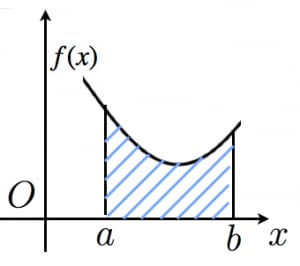
なぜ定積分で面積が求まるのか 高校数学の美しい物語

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

自然科学のための数学14年度第12講

符号付きの面積ってなに ー定積分で面積がマイナスになる理由 Litetube

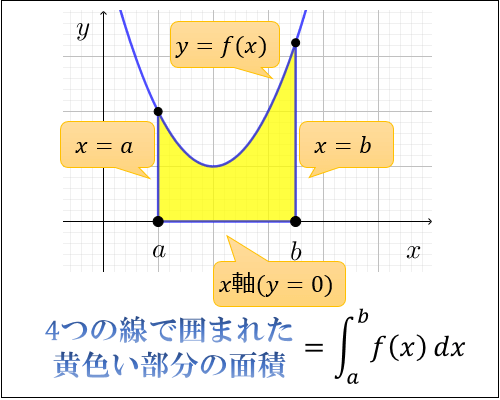
積分とは何なのか 面積と積分計算の意味 アタリマエ

数学定積分で答えがマイナスになることがありますが なぜですか 定 Yahoo 知恵袋

積分の面積公式を分かりやすく解説 まず理解して覚えよう 大学生の勉強部屋

積分の問題でたまに面積がマイナスになる 18年03月01日のその他のボケ ボケて Bokete

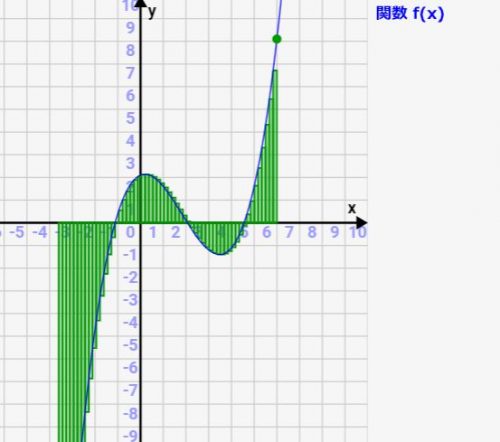
積分の意味を 面積 で捉えよう シミュレーターで理解を深めよう 数学入門

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

積分してwi Fiをつなげよう 大人のための数学教室 和 Note

裏ワザ 積分せずに面積を一瞬で求める 6分の1公式 3分の1公式 12分の1公式 とは 使い方をて解説 ますますmathが好きになる 魔法の数学ノート

裏ワザ 積分せずに面積を一瞬で求める 6分の1公式 3分の1公式 12分の1公式 とは 使い方をて解説 ますますmathが好きになる 魔法の数学ノート

絶対値記号を含む定積分 数学 苦手解決q A 進研ゼミ高校講座

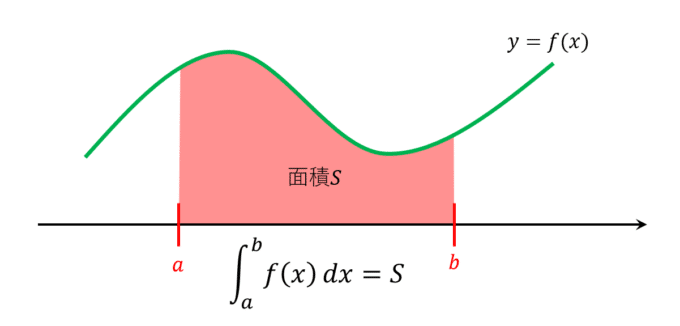
定積分によって面積を求める問題の解き方と公式

電気の基礎知識 数学の基礎知識 2 株式会社アイティ オフィス

面積の計算について 数学 苦手解決q A 進研ゼミ高校講座

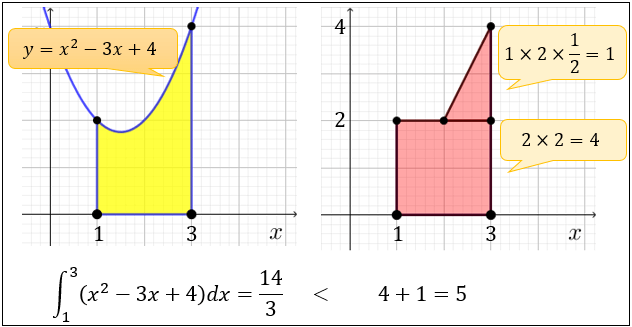
積分とは何なのか 面積と積分計算の意味 アタリマエ

基本 曲線とx軸の間の面積と積分 なかけんの数学ノート

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

1 6公式の使い方 思考力を鍛える数学

台形公式

何故面積はマイナスにならないのですか Quora

定積分 面積がマイナス Youtube

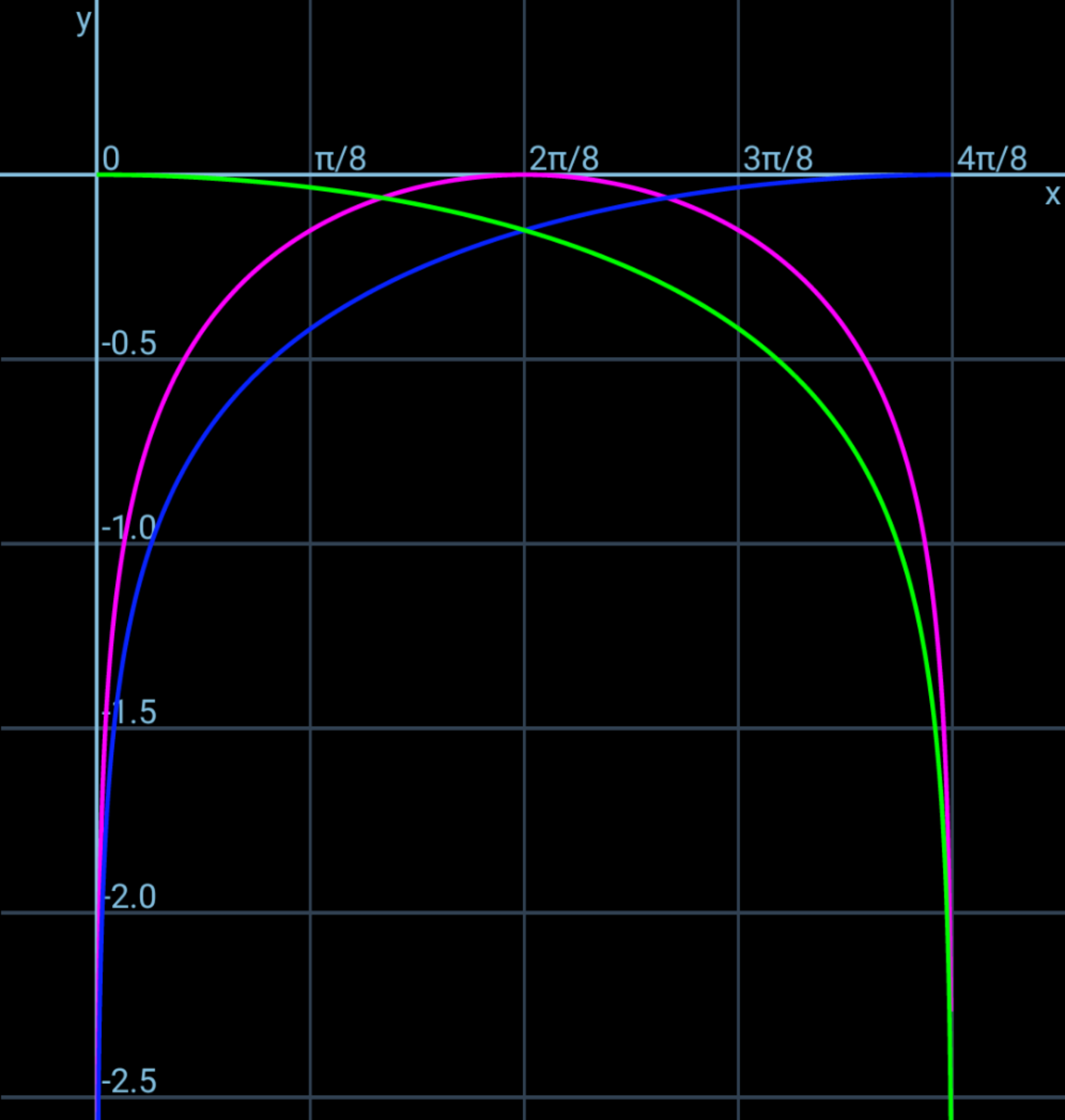
解析学演習 49 4 広義積分と面積 齊藤数学教室 算数オリンピックから大学数学入門

被積分関数が絶対値付きの定積分 数学の偏差値を上げて合格を目指す

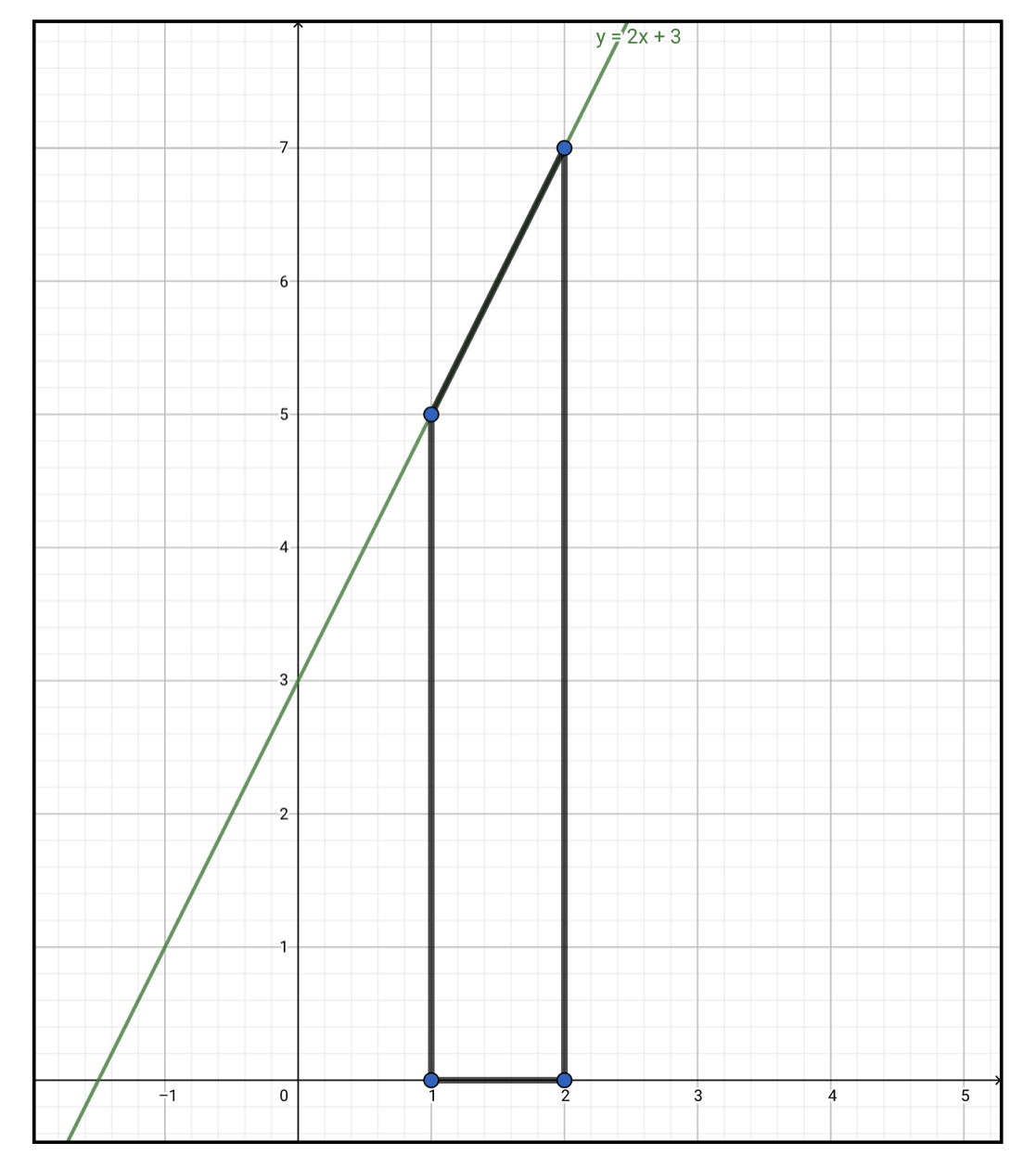
定積分のイメージ ぽこラボ勉強ブログ

面積を積分して求めた時に答えがマイナスになってしまったら 面積がマイナスになる訳無 Clear

ここから 方向を含む面積積分の話 Ppt Download

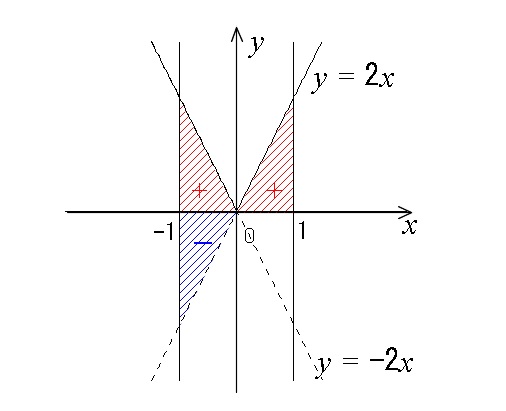
定積分によって面積を求める問題の解き方と公式

48s96ub7b0z5f Net Teisekibun Menseki Kihon

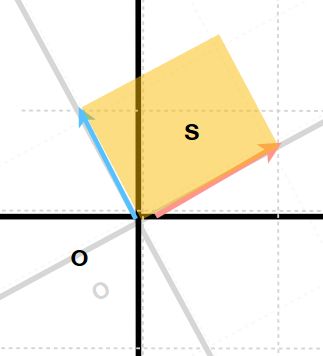
なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学

積分の意味を 面積 で捉えよう シミュレーターで理解を深めよう 数学入門

1 赤で丸印をつけた部分はなぜ 急にマイナスが出てくるのですか Clear

Incoming Term: 積分 面積 マイナスになる,